External Merge Sort using Priority Queue

External Sorting — Totoro.

External sorting is a class of sorting algorithms that can handle massive amounts of data. External sorting is required when the data being sorted does not fit into the main memory of a computing device (RAM). Instead, they must reside in the slower external memory (Disk).

To explain the working of External Merge Sort using a Priority Queue, consider the input array: [5, 8, 6, 3, 7, 1, 4, 9, 10, 2]

Overview: In the Split Phase, the large input file is split into smaller chunks that can be fit into the memory. In the Merge Phase, perform K-way merge with each smaller chunk file one after the other and write the output to a file.

Split Phase:

Split the input into chunks (5 chunks).
Then, sort each of the individual chunks.
Finally, store the sorted chunks in files (5 temporary files).

Doing so, we have 5 files with:

Chunk 1: [5, 8] Chunk 2: [3, 6] Chunk 3: [1, 7] Chunk 4: [4, 9] Chunk 5: [2, 10]

Merge Phase:

Create m number of HeapNode(s), where the value of the HeapNode is the chunk’s lowest element, and store the reference to the temporary chunk file.

Example:

{
	"element": 5,
	"file": <chunk-file>
} 

Now, store all the m HeapNode(s) in a Min Heap, where the top node is always the minimum element in the heap:

Perform the heapify operation -> store the element in an output file -> replace the min element with the next element in the chuck file, which owns min element
Pick the min element in the min-heap 1 and write it to an output file 1
Find the next element in the chunk file, which owns min element 1
Number 7 from Chunk 3; move it to the heap and perform heapify

      7                                    2
    /  \                                 /  \
   2     5      Heapify -->             3    5	
  /  \                                 / \
 4    3                               4   7 

Pick the min element 2 and append it to output file 1, 2
Find the next element in the chunk file, which owns min element 2
Number 10 from Chunk 5; move it to the heap and perform heapify

      10                                   3
    /  \                                 /  \
   3     5      Heapify -->             4    5	
  /  \                                 / \
 4    7                               10   7 

Pick the min element 3 and append it to output file 1, 2, 3
Find the next element in the chunk file, which owns min element 3
Number 6 from Chunk 2; move it to the heap and perform heapify

      6                                   4
    /  \                                 /  \
   4     5      Heapify -->             6    5	
  /  \                                 / \
10   7                               10   7 

Pick the min element 4 and append it to output file 1, 2, 3, 4
Find the next element in the chunk file, which owns min element 4
Number 9 from Chunk 4; move it to the heap and perform heapify

      9                                   5
    /  \                                 /  \
   6     5      Heapify -->             6    9	
  /  \                                 / \
10   7                               10   7 

Pick the min element 5 and append it to output file 1, 2, 3, 4, 5
Find the next element in the chunk file, which owns min element 5
Number 8 from Chunk 1; move it to the heap and perform heapify

      8                                   6
    /  \                                 /  \
   6     9      Heapify -->             7    9	
  /  \                                 / \
10   7                               10   8 

If the next element in the chunk file is smaller than the current min element, replace the min element in MAX_INTEGER and repeat the process until all the elements in the heap are MAX_INTEGER
Pick the min element 6 and append it to output file 1, 2, 3, 4, 5, 6
Find the next element in the chunk file, which owns min element 6
When you see EOF (End of Line), replace it with MAX_INTEGER

   MAX_INT                                 7
    /  \                                 /  \
   7    9      Heapify -->              8     9	
  /  \                                 / \
10   8                               10   MAX_INT

Continue until the heap looks like:

                       MAX_INT                       
                        /   \
                    MAX_INT  MAX_INT
                    /    \                         
                 MAX_INT MAX_INT        

The final output: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 😎

Since you are anyway here, Checkout sorting-algorithms 🚀 to compare sort algorithms; here’s a comparison of the external sort with in-memory merge sort.

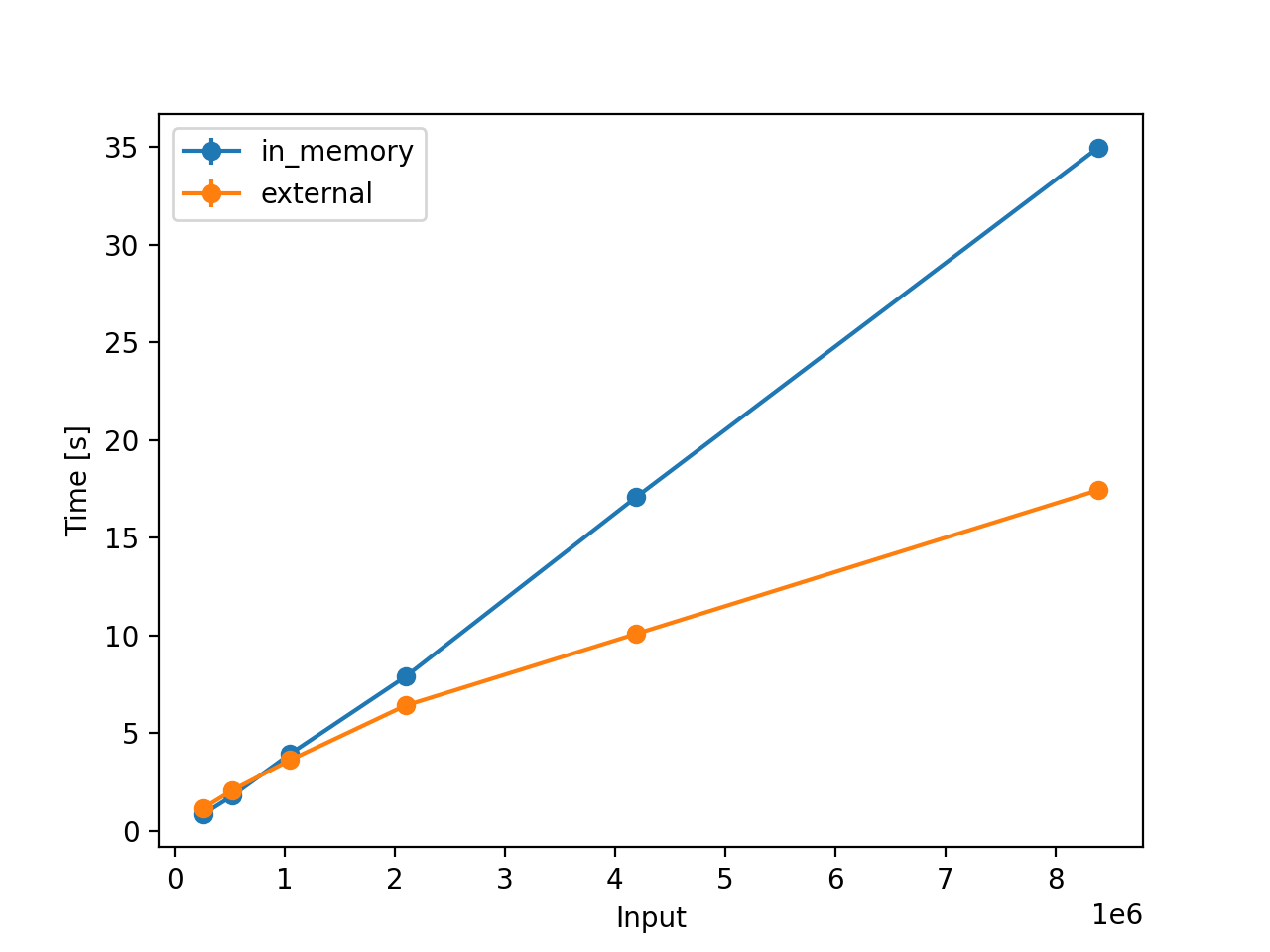
Figure 1: For Powers of 2

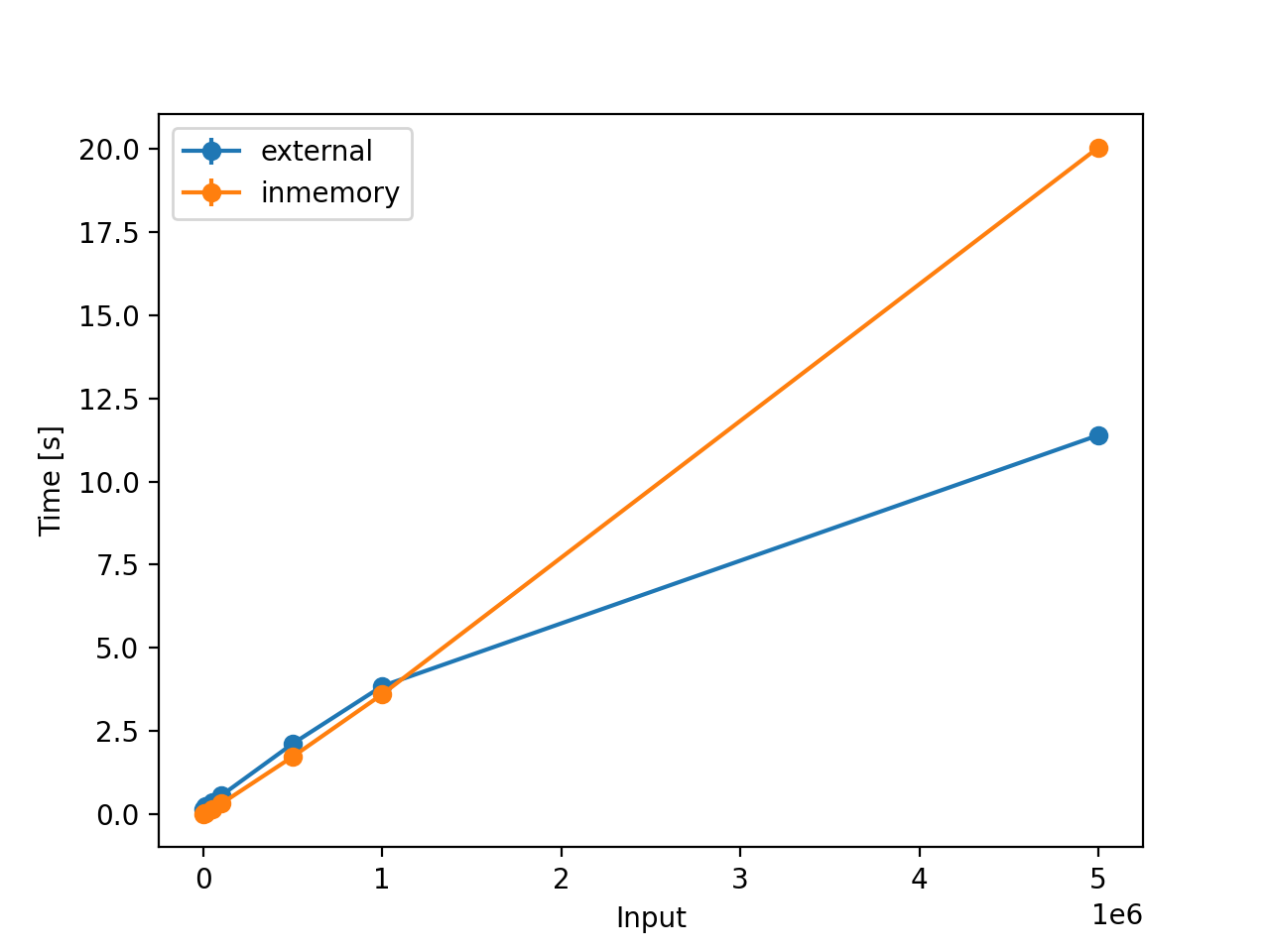
Figure 2: For Powers of 10

Split Phase:

Merge Phase:

About Adesh Nalpet Adimurthy